
Puzzles as a whole are highly beneficial for cognitive development due to the fact that they train parts of the brain which are not always put to use in day-to-day life. Tangram puzzles expand on this idea as not only do they work to enhance a student’s spatial reasoning ability, but they also offer endless possibilities to exercise a student’s existing knowledge, introduce new vocabulary or ideas, and practice several other skills. This is especially true in the math classroom, particularly for Primary and Lower Secondary school students.
Tangram puzzles are composed of seven shapes, which have the potential to be arranged together into a square. However, a square is just one of the many shapes that can be made from the pieces provided and presents just one small step of an entire tangram lesson that can be implemented into the curriculum for students of many ages. For the purposes of this article, we will assume a first-grade classroom, with students mostly ranging from six to seven years old. However, some chances and opportunities to scale the exercise up for older or more advanced students will be provided as well.
Background on Tangrams
First it is important to gain the interest of the students, while also offering a practical – albeit fictional – example of what they are about to learn in real life. It is here that the legend of the origins of the tangram can be told. There are many good young children’s books that do a great job telling a longer more detailed version, or simply refer to our past blog post on the matter: A History of Tangrams.
Introducing the Tangram
Now that the topic has been introduced and the students know what to expect, it is a good time to introduce the tangram itself. This often works well when done with the entire class as a group. Each piece can be presented to the class, and students can provide observations they made regarding each piece. For example, you might hold up the triangle F from below.
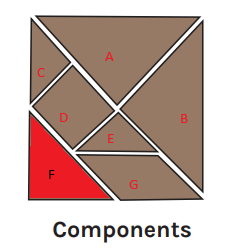
Students will then raise their hands and offer information to the effect of: “It’s a triangle”, “It has three sides”, “It has three angles”, or they may even compare the pieces to each other, saying “It’s bigger than the triangle C”.
During this part of the lesson, it is a great opportunity for you to review existing geometric vocabulary, correct vocabulary mistakes, and even introduce some new ones depending on the prior knowledge of the students. Older or more advanced classes might comment on the types of triangles, the acuteness of some of the angles, or supplementary and complementary angles within the parallelogram.
Solving the Tangram
It is here that we recommend breaking from the class group, and letting the students commence trying to complete the tangram on their own. At this point, with younger students, it’s often a good idea to pair them with partners so that they have help, as well as the opportunity to use their teamworking, vocabulary, and cooperation skills. Students can often be heard communicating with their partners, saying things like “rotate that triangle”, “flip the parallelogram”, or “move the square to the right”.
The process of completing the tangram relies on lots of trial and error. Playing around for a bit to see what works and proceeding from there. Discovering the relationships between all the shapes and coming to understand how they all fit together into one larger piece. It teaches spatial reasoning and geometrical imagination in a way that only sitting there, feeling the shapes in their hands, and trying to fit them in the square really can.
Exploring Further
At this point, the tangram has successfully been introduced to your classroom. Students should either be silently trying to complete the tangram on their own, or cooperatively working with their partner to get it done as a team. Regardless, once the class finishes up assembling their tangrams back into the original square, there are a few other routes that the lesson can take and that is all up to you.
Perhaps you decide you want to call out the name of a shape and have the students assemble the shape with the pieces they have in front of them. Once called on, students can show their solutions to the class. From here it can be seen just how many different ways to make certain shapes there are. This offers the chance for review questions like:
-
- What shapes can be combined to make a triangle?
-
- What two shapes can be combined to make a square?
-
- What were the original seven shapes that compose the square?
-
- What do you notice about the different triangles we have?
These questions allow the students to think critically about the tangram and what they have been working on.
Another possible route could be to call out a pattern or an image and ask the students to do their best to construct it with the tangram’s shapes. This will really put their imaginations to work as they try not only to compose their own image, like a dog for instance. Students must also try and understand their classmates’ shapes as well. To see what shapes their classmates used for the head, or how they constructed the tail and so on. For this activity in particular, we recommend outlining a few rules prior to beginning. The first being that all seven pieces must be in use for every shape. Also, that the pieces cannot overlap or rest on top of each other. Lastly it’s important to clarify that the pieces can be flipped upside down and turned over as needed.
Concluding
The tangram puzzle is an excellent tool for teaching and improving skills on an individual level, but where it really excels is in a classroom or group setting. Tangram puzzles do an excellent job expanding one’s skills in spatial reasoning and geometry, but it goes further than that when taught at the classroom level. Each of these introductory tactics to involve the tangram into a class plays into the idea of differing perspectives and solutions. Allowing for multiple opinions, solutions, and points of view to be on display. Which serves the unique purpose of forcing the student to understand the literal and physical different angles to approach a problem from.
